

Assignment 6:
Should a Field Goal Kicker Ever Take a Penalty?
By: Stephen Morgan

In the game of football, one way a team can score points is by having their team attempt to kick a field
goal. When this is done, the team's kicker lines up 17 yards back from where the team last had the ball. The
ball is placed on the according hash mark, where a kick is attempted (i.e. if the team is on the 1-yard line, the kicker
would attempt an 18-yard field goal). In today's game a field goal is worth 3 points. The ball has to be kicked
through a goal post that is 18 feet, 6 inches wide. However, this was not always the case.
In 1883, a field goal counted for 5 points. This was eventually reduced to 4 points in 1904, and 3 points in
1909. In 1959, the goalposts in collegiate football were widened to 23 feet, 4 inches. However by 1991,
they were reduced to 18 feet, 6 inches. Though this caused extreme angles for short field goal attempts. So in 1993,
the distance between hashmarks were reduced from 53 feet, 4 inches apart, to their current 40 feet. These are still the
measurements today. The endzones are 10 yards long.
As an interesting aside, the longest field goal made in NCAA history was 69 yards. It was made by John
Eizell of Abliene Christian on October 16, 1976.
(Information from: http://en.wikipedia.org/wiki/Field_goal_(football)#Collegiate, 23 September, 2010).
Assignment 6 Prompt:
The football rules in college football were changed a few years ago have made the uprights 5 feet narrower
than previously. Many game commentators have harped about how much harder it is to kick field goals
from the hash marks. Assume the field goal is attempted from the hash marks. At what yard marker does
the kicker have maximum angle to the two uprights. Note: You will need to find out the width of the
uprights and the width of the hash marks .. . make a sketchpad model. Is there any merit to some
commentators argument to take a penalty in order to have a "better angle" on the field goal kick?
Assignment 6 Solution:
The first thing I did when approaching this problem was to construct a picture of the situation that we are
trying to examine. Here is a GSP Sketch illustrating the idea. I also thought that creating the following
picture below would help us allow us to think better about the task at hand.
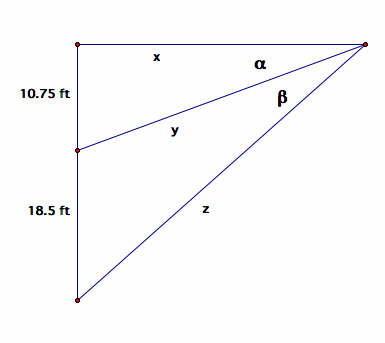
Above us is a picture of a triangle illustrating the situation from the kicker's point of view we can observe several things.
First, since the kicker is lined up with the hash mark the kicker is 10.75 feet away from being horoziontally lined up (angle alpha) with
the field goal post (40=18.5+10.75+10.75). *We assume the goal post is in the middle of the field. Secondly, we can
see the kicker's angle with the goal post (beta) will be generated by a triangle with a height 10.75 feet and length x (the distance from
the field goal) combined with the triangle that has the angle of incidence from the kicker to the field goal and height 18.5 feet,
the distance of the goal post. The combined two triangles form the right triangle above.
This is convienant for us, since it allows us to use trigonometry and calculus to find the maximum angle (i.e. where the kicker would
have the easier time kicking a field goal if leg strength does not matter), if we know the distance we are from the field goal.
From this we are able to generate the angle as a function of x.
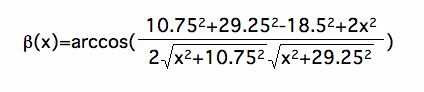
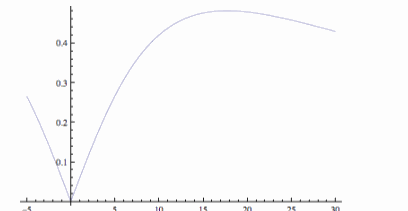
Using Calculus, we can solve for x and beta. When we do this we find out that beta=27.6 degrees and x is 17.7 feet. However since a field goal
kicker cannot kick a field goal less then 51 feet (17 yards) this fact does not matter. However, we can look at the derivative of our function.
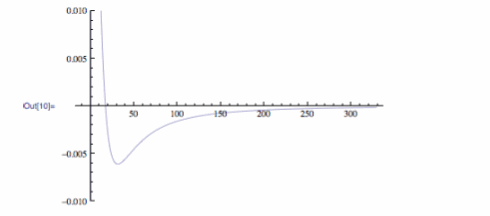
When I did this I looked at the derivative for values larger then 17.7 feet for x. They all ended up being negative, meaning that as the kicker
moves further away, the angle will decrease. This means that assumingleg strength does not matter, that the further away the kicker is from
the field goal, the harder it will be to make the kick, since the angle will be smaller. Therefore, it is impossible for a kicker to kick a field goal at
this distance. The goal posts are at the end of the end zone which is 10 yards from the goal line. Since 10 yards equals 30 feet>17.7 feet, a kicker
can never kick a field goal from this distance. Therefore, a kicker should never take a penalty.
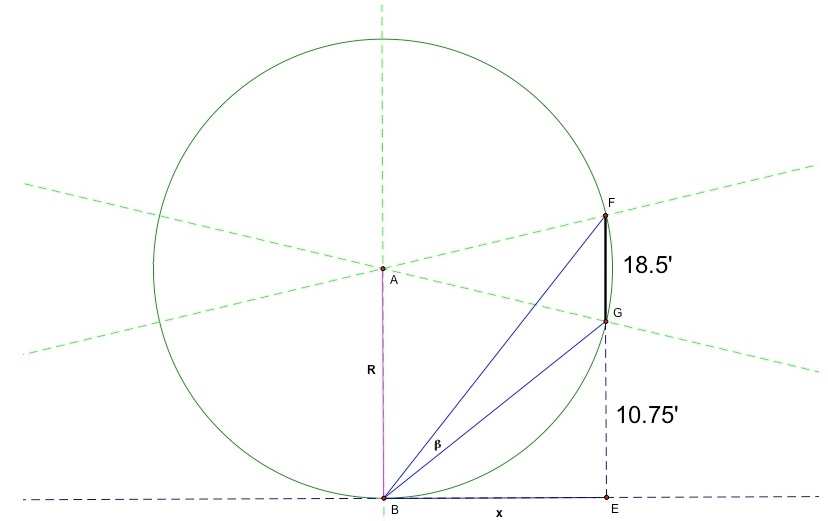
Another way we can look at this problem is with circles. We can consider the point of the ball placement and two points, one on each side of the goal
posts. Three points determine a circle and the 18.5 foot distance between the goal posts is a fixed chord of the circle formed by the three points. The circle changes
in size as the point of the ball is moved along the hash mark.
But, the circle would also intersect the hash mark in a second point and the angle would be the same since the inscribed angle theorem says that all angles inscribed
in a circle subtending the same chord are equal in measure. The circle will be the largest, and hence the angle a maximum, when the circle is tangent to the hash line.
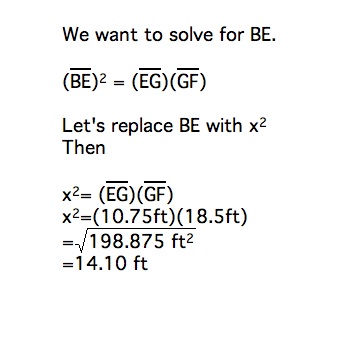
Even though this is several feet off of the other solution, we would still have to kick the field goal in the end zone. Since that is illegal the kicker should never accept a penalty
when attempting a field goal.